¿Que es un grafo?
Los grafos son un conjunto de puntos, de los cuales algún par de ellos está conectado por unas líneas. Si estas líneas son flechas, hablaremos de grafo dirigido (digrafo), mientras que si son simples líneas estamos ante un grafo no dirigido.
Más formalmente se pueden definir como un conjunto de vértices y un conjunto de aristas. Cada arista es un par (u,v), donde u y v pertenecen al conjunto de vértices. Si este par es ordenado el grafo es dirigido.
Vamos a ver un par de ejemplos:
Grafo no dirigido
Grafo dirigido.
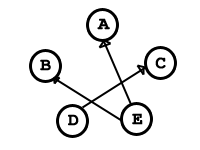
¿Para que sirve los grafos?
Los campos de utilización de los grafos son muy varidos, ya que los vértices pueden representar cualquier elemento (ciudades, aeropuertos, pc's...), y las aristas serían la conexión entre esos elementos (carreteras, pasillos aéreos, redes...). Por lo tanto los grafos son muy usados en la modelización de sistemas reales.
Adyacencia.
Existe adyacencia entre 2 vertices si estan unidos por un arco.
Incidencia.
EL ARCO INCIDE ENTRE A Y B
EL ARCO INCIDE EN EL VERTICE B
Clases de grafos
Grafos y digrafos fuertemente conectados
Un grafo o digrafo esta fuertemente conectado si desde cualquier vertice se puede llegar a los demas
Grafo de camino simple
un grafo es de camino simple si partiendo de cualquer vertice podemos recorrer toda la estructura sin repetir arcos ni vertices
Grafo euleriano
Un grafo es euleriano si partiendo de cualquier vértice podemos recorrer todos los arcos llegando de nuevo al vertice origen, se pueden visitar los vértices cuantas veces sea necesario los arcos se pueden recorrer una sola vez.
Grafo hamiltoniano
Un grafo es hamiltoniano si partiendon de cualquier vertive podemos recorrer todos los vertices sin repetir ninguno, y finalmente llegar al vertice origen
Grados de un vertice
El grado de un vertice es igual al numero de arcos que inciden en ese vertice
Tabla.
Grado de un dígrafo.
Tabla.
Grafo regular
Grafo con arco ciclico
Multigrafo
Un grafo es multigrafo cuando se acepta más de un arco uniendo dos vértices. En términos formales, no son grafos. Un multígrafo es un grafo que consta de segmentos múltiples y lazos.
Matriz de adyasencia
Un grafo se puede representar mediante una matriz. Es la forma más sencilla de representar un grafo. A esta matriz se le denomina matriz de adyacencia. la matriz de adyacensi se trabaja con 0 y 1 osea que es binaria si ponemos un 1 es por que existe un camino o un arco que incide en esos vertices si es 0 es por que lo lo hay, generalmente la diagonal principal de la matriz son 0 por que no hay ningún camino que salga de un vertice y llegue al mismo a excepción de los grafos ciclicos
Lista de adyacensia.
Es una representación de todas las aristas o arcos de un grafo mediante una lista.
si el grafo es no dirigido, cada entrada es un conjunto o multiconjunto de dos vertices conteniendo los dos extremos de la arista correspondiente. si el grafo es dirigido, cada entrada es un a tupla de dos nodos, uno denotando el nodo fuerte y el otro denotando el nodo destino del arco correspondiente
Es una representación de todas las aristas o arcos de un grafo mediante una lista.
si el grafo es no dirigido, cada entrada es un conjunto o multiconjunto de dos vertices conteniendo los dos extremos de la arista correspondiente. si el grafo es dirigido, cada entrada es un a tupla de dos nodos, uno denotando el nodo fuerte y el otro denotando el nodo destino del arco correspondiente
Lista de adyacencia del grafo anterio
"El siguiente articulo fue elaborado por un estudiante de Ingeniería de Sistemas de la Universidad Incca de Colombia"
Algoritmo de Prim
El
algoritmo de Prim consiste en recorrer todos los vértices de un grafo en el
menor peso posible, esto genera un árbol recubridor de menor peso, para que
esto se cumpla el grafo debe ser conexo, estar etiquetado y sus arcos deben de
tener un peso. Es decir:
Si
observamos el arco que hay entre el vértice 0 y 2 tiene un numero en rojo, eso
es lo que llamamos “peso” luego también es un grafo conexo y esta etiquetado.
En
el algoritmo de Prim podemos comenzar por cualquier vértice luego para
recorrerlo hay que tener los vértices adyacentes al que hemos escogido como
punto de partida es decir, si empezamos con el vértice “0” este tiene dos
vértices adyacentes que son el “2” y el “3”.
Entonces
para saber a cuál de los dos escoger, entre el vértice “2” o “3” miramos el
peso que tiene cada arco. Así el peso del vértice “0” al vértice “2” es de 5, y del vértice “0” al vértice
“3” es de 8 entonces
simplemente escogemos el de menor peso que es del vértice “0” al vértice “2” y
ya tenemos trazado un arco. Así tenemos que hacer el mismo proceso para los
demás vértices hasta completar todo el grafo, hay que tener en cuenta que al
hacer el árbol recubridor, este no puede quedar cerrado por que quedaría como
un ciclo y no queremos eso. Aquí tendremos un ejemplo…
El
código para el algoritmo de Prim seria:
#include "stdio.h"
#include "conio.h"
#include "stdlib.h"
#define MAXIMO 20
#define PR(x) printf ("%s",x)
#define SALTO printf ("\n")
int main() {
int M[MAXIMO][MAXIMO],T[MAXIMO][MAXIMO];
int suma, marcas[MAXIMO],padres[MAXIMO],minimo [MAXIMO];
int nv,i;
int PRIM (int
M[][MAXIMO],
int
N,int minimo[],int padres[],int marcas[]);
int lea_grafo (int
grafo[][MAXIMO]);
void listar_g (int
g[][MAXIMO], int nv);
void listar_r (int
a[],int nv);
nv = lea_grafo (M);
listar_g (M ,nv);
SALTO;
getch();
suma = PRIM (M,nv,minimo,padres,marcas);
printf ("\n suma=%d\n",suma);
SALTO;
listar_r (minimo,nv);
SALTO;
SALTO;
listar_r (padres,nv);
SALTO;
listar_r (marcas,nv);
SALTO;
getch();
}
int PRIM (int M[][MAXIMO],int N,int minimo[],int padres[],int marcas[])
{
int min;
int j,k,escogido,suma;
for (j=1; j<=N; j++ ) {
minimo[j] = M[1][j];
marcas [j] = 0;
padres [j] = 1;
}
minimo [1] = 0;
padres [1]= 0;
marcas [1] = 1;
suma = 0;
for (k = 2; k <= N;
k++) {
min =
32767;
for (j=1; j
<= N; j++)
if (marcas [j] == 0 && minimo [j] <
min) {
min = minimo [j];
escogido = j;
}
marcas [escogido] = 1;
suma = suma + min;
for (j=1; j <= N; j++)
if
(marcas [j] == 0 &&
M[escogido][j] < minimo[j] ) {
minimo [j] =
M[escogido][j];
padres [j] = escogido;
}
}
return (suma);
}
int lea_grafo (int grafo[][MAXIMO])
{
int
v,ad,i,j,n,costo,lea();
PR("De numero de vertices...");
SALTO;
n = lea();
for (i=1; i <= n;
i++)
for (j=1; j
<=n; j++)
grafo[i][j]
= 32767;
PR ("Vertice ... ");
v = 1;
printf ("%d",v);
SALTO;
while (v <= n) {
PR ("Lea el primer adjunto al vertice
");
printf ("%d ",v);
PR(". 99 para terminar");
SALTO;
ad = lea();
while (ad
!= 99) {
PR("Lea costo del arco");SALTO;
costo = lea();
grafo [v][ad] = costo;
PR ("Lea otro adjunto al
vertice ");
printf ("%d ",v);
PR(". 99 para
terminar");
SALTO;
ad
= lea();
}
PR
("Vertice ...");
v++;
printf
("%d ",v);
SALTO;
}
return (n);
}
int lea() {
char L[10];
gets (L);
return (atoi (L));
}
void listar_g (int g[][MAXIMO], int nv) {
int i,j;
for (i=1; i <= nv;
i++) {
for (j = 1;
j <= nv; j++)
if
(g[i][j] == 32767)
printf
("%s"," * ");
else
printf ("%2d ",g[i][j]);
SALTO;
}
}
void listar_r (int a[],int nv) {
int k;
for (k=1; k<=nv;
k++)
printf
("%d ",a[k]);
}
ALGORITMO DE WARSHALL
Es un algoritmo de análisis
sobre grafos para encontrar el camino mínimo entre un par de vertices, como
resultado nos da la mejor ruta para poder llegar al vértice destino en grafos
dirigidos Como resultado nos dara una matriz de clausura transitiva.
PASOS
1) Hallamos la
matriz de adyacencia.
2) Tomamos cada vértice como pivote llenando su
respectiva matriz dependiendo si hay
camino o no
3) Como resultado nos da una matriz de adyacencia
transitiva con la cual podemos saber si hay un camino de un vértice cualquiera
a otro vértice elegido al azar
PIVOTE=cuando se dice
tomamos el vértice como pivote quiere decir que podemos formar una conexión
directa entre un vértice y un tercero, como
si el vértice tomado como pivote no estuviera
· Matriz de adyacencia.
a
|
b
|
c
|
D
|
|
a
|
0
|
1
|
0
|
0
|
b
|
0
|
0
|
1
|
0
|
c
|
1
|
0
|
0
|
1
|
d
|
0
|
0
|
0
|
0
|
· Tomamos como pivote a (a)
M1 (a)
a
|
b
|
c
|
D
|
|
a
|
0
|
1
|
0
|
0
|
b
|
0
|
0
|
1
|
0
|
c
|
1
|
1
|
0
|
1
|
d
|
0
|
0
|
0
|
0
|
· Tomamos como pivote a (b) sin olvidar que (a)
sigue siendo pivote
M2 (b)
a
|
b
|
c
|
D
|
|
a
|
0
|
1
|
1
|
0
|
b
|
0
|
0
|
1
|
0
|
c
|
1
|
1
|
1
|
1
|
d
|
0
|
0
|
0
|
0
|
· Tomamos como pivote a (c) sin olvidar que los anteriores vértices
siguen siendo pivotes en este caso (a) y
(b)
M3 (c)
a
|
b
|
c
|
D
|
|
a
|
1
|
1
|
1
|
1
|
b
|
1
|
1
|
1
|
1
|
c
|
1
|
1
|
1
|
1
|
d
|
0
|
0
|
0
|
0
|
· No realizamos la matriz con el pivote (d) ya
que no tiene ningún arco de adyacencia
por lo tanto la matriz serian ceros ( 0
)
· Matriz de clausura transitiva.
a
|
b
|
c
|
D
|
|
a
|
1
|
1
|
1
|
1
|
b
|
1
|
1
|
1
|
1
|
c
|
1
|
1
|
1
|
1
|
d
|
0
|
0
|
0
|
0
|
CODIGO
#include
"stdio.h"
#include
"stdlib.h"
#include
"conio.h"
#include
"alloc.h"
#define MAXIMO 20
#define PR(x) printf
("%s",x)
#define SALTO printf
("\n")
void main() {
int
M[MAXIMO][MAXIMO],T[MAXIMO][MAXIMO];
int nv,i;
void listar_g (int g[][MAXIMO], int
nv);
int lea_grafo (int grafo[][MAXIMO]);
void WARSHALL (int M[][MAXIMO], int
T[][MAXIMO], int nv);
nv = lea_grafo (M);
listar_g
(M ,nv);
SALTO;
getch();
WARSHALL (M,T,nv);
listar_g (T,nv);
SALTO;
getch();
}
void WARSHALL (int M[][MAXIMO],
int T[][MAXIMO], int nv)
{
int i,j,k;
void listar_g (int g[][MAXIMO], int
nv);
void copiar (int a[][MAXIMO], int
b[][MAXIMO],int nv);
copiar (T, M, nv);
for (k=1; k<=nv; k++) {
for (i=1; i<=nv; i++)
{
if (i!=k) {
if
(T[i][k] == 1) {
for
(j=1; j<=nv; j++) {
if
(T[i][j] == 0)
T[i][j]
= T[k][j];
}
}
}
}
SALTO;
listar_g
(T,nv);getch();
SALTO;
}
}
int lea_grafo (int
grafo[][MAXIMO])
{
int v,ad,i,j,n;
int lea();
PR("De
numero de vertices...");
SALTO;
n = lea();
for (i=1; i <= n; i++)
for (j=1; j <=n; j++)
grafo[i][j] =
0;
PR ("Lea el primer
vertice. 99 para terminar...");
SALTO;
v =
lea();
while (v
!= 99) {
PR
("Lea el primer adjunto al vertice ");
printf
("%d ",v);
PR(".
99 para terminar");
SALTO;
ad = lea();
while (ad != 99) {
grafo
[v][ad] = 1;
PR
("Lea otro adjunto al vertice ");
printf
("%d ",v);
PR(".
99 para terminar");
SALTO;
ad
= lea();
}
PR
("Lea otro vertice. 99 para terminar...");
SALTO;
v
= lea();
}
return (n);
}
int lea() {
char L[10];
gets (L);
return (atoi (L));
}
void listar_g (int
g[][MAXIMO], int nv) {
int i,j;
for (i=1; i <= nv; i++) {
for (j = 1; j <= nv;
j++)
printf
("%d ",g[i][j]);
SALTO;
}
}
void copiar (int a[][MAXIMO], int b[][MAXIMO],int nv) {
int i,j;
for (i=1; i<=nv; i++)
for (j=1; j <= nv;
j++)
a[i][j] =
b[i][j];
}
"El siguiente articulo fue elaborado por un estudiante de Ingeniería de Sistemas de la Universidad Incca de Colombia"
Algoritmo de Kruskal
El algoritmo de kruskal es un algoritmo de
recubrimiento mínimo conexo ponderado, o sea que va unir todos los nodos
formando un árbol, tomando las aristas que tengan un peso que siempre sea
menor.
Este
árbol de un grafo es un sub-grafo que contiene todos sus vértices o
nodos. Un grafo puede tener múltiples árboles.
CARACTERÍSTICAS
· Algoritmo basado en las aristas
· Agregar las aristas , uno a la vez, en
orden de peso creciente
· El objetivo del algoritmo de Kruskal es
construir un árbol (sub-grafo sin ciclos) formado por arcos sucesivamente
seleccionados de mínimo peso a partir de un grafo con pesos en los arcos.
-Resuelve la misma clase de problemas que el de Prim, a diferencia que no se escoge un nodo al azar.
-Resuelve la misma clase de problemas que el de Prim, a diferencia que no se escoge un nodo al azar.
·
Trabaja con grafos ponderados, y no
dirigidos.
EJEMPLO:
CODIGO:
#include
<iostream>
#include
<string>
#include
<vector>
#include
<algorithm>
#include <list>
#include<stdio.h>
#define REP(i,a) for(i=0;i<a;i++)
#define FOR(i,a,b)
for(i=a;i<b;i++)
#define ii
pair<int,int>
using namespace std;
vector<int>
pset;
vector<pair<int,ii>
>grafo;
void initSet(int
size)
{
int i;
pset.resize(size);
REP(i,size+1)
pset[i]=i;
}
int findSet(int i)
{
return (pset[i]==i)?
i:(pset[i]=findSet(pset[i]));
}
void unionSet(int
i,int j)
{
pset[findSet(i)]=findSet(j);
}
bool isSameSet(int
i,int j)
{
if(findSet(i) == findSet(j))
return true;
return false;
}
void kruskal(int N)
{int sum=0,i;
initSet(N);
sort(grafo.begin(),grafo.end());
for(i=0;i<grafo.size();i++)
{ pair<int,ii>aux=grafo[i];
if(!isSameSet(aux.second.first,aux.second.second))
{
cout<<"pasa en:
"<<aux.second.first<<","<<aux.second.second<<endl;
sum=aux.first+sum;
unionSet(aux.second.first,aux.second.second);
}
}
cout<<"el
peso"<<sum;
}
int main(){
int V,A,i,a,b,w;
cout<<"\t\tAlgoritmo
de kruskal"<<endl;
cout<<"ingrese numero de
aristas"<<endl;
cin>>A;
cout<<"ingrese numero de
vertices"<<endl;
cin>>V;
cout<<"ingrese desde que vertice a que vertice:
"<<endl;
for(i=0;i<A;i++){
cout<<"Del
vertice: "; cin>>a; cout<<"al vertice:
";cin>>b;
cout<<"su peso: ";
cin>>w;
grafo.push_back(pair<int,ii>(w,ii(a,b)));
}
kruskal(V);
system
("PAUSE");
return 0;
}
"El siguiente articulo fue elaborado por un estudiante de Ingeniería de Sistemas de la Universidad Incca de Colombia"
Es un algoritmo de análisis
sobre grafos para encontrar el camino mínimo en grafos dirigidos ponderados. El
algoritmo encuentra el camino entre todos los pares de vértices en una única
ejecución. El algoritmo de Floyd es un ejemplo de programación dinámica.
El algoritmo de Floyd es más
importante desde el punto de almacenamiento dado que puede ser implementado una
vez se halla actualizado la distancia de la matriz.
Lo siguiente es coger una columna con una fila
y sumarla, si la suma de la fila y la columna es menor que el número que
está en la posición evaluada se cambia
pero si es mayor no se cambia. Si hay un infinito en la posición evaluada también
se cambia por el número que haya dado la suma.
Teniendo en cuenta que no se puede sumar un infinito con
otro número u otro infinito.
En la matriz de padres se coloca la letra que se está
evaluando que es de donde proviene el número que se puso en la matriz de
caminos.
Para saber cuál es el camino que tiene menor peso para
llegar de la A a la E se mira en la última matriz de padres entonces para
llegar a la E tiene que pasar por la C que es la letra que esta subrayada y si
vemos es la que menor peso tiene para llegar a esta esto se ve en la matriz de
camino. Otro ejemplo es para llegar de la E a la C tiene que pasar por la B que
es la letra subrayada y también es el menor peso por el cual se puede ir lo
podemos observar en la matriz de caminos.
CODIGO:
#include "stdio.h"
#include "conio.h"
#include "stdlib.h"
#define MAXIMO 20
#define PR(x) printf ("%s",x)
#define SALTO printf ("\n")
int main() {
int M[MAXIMO][MAXIMO];
int nv;
int lea_grafo (int
grafo[][MAXIMO]);
void listar_g (int
g[][MAXIMO], int nv);
void FLOYD (int
M[][MAXIMO],int N);
nv = lea_grafo (M);
listar_g
(M ,nv);
SALTO;
getch();
FLOYD
(M,nv);
SALTO;
listar_g (M,nv);
getch();
}
void FLOYD (int M[][MAXIMO],int N)
{
int i,j,k;
void listar_g (int
g[][MAXIMO], int nv);
for (k=1; k <= N; k++)
M [k][k] =
0;
for (k=1; k <= N;
k++) {
for (i=1; i
<= N; i++) {
if
(i != k) {
if
(M [i][k] != 32000) {
for
(j=1; j <= N; j++) {
if
(M[i][k] + M[k][j]
<
M[i][j] )
M[i][j]
=
M[i][k]+
M[k][j];}}}}
SALTO;
listar_g
(M,N);
getch();}}
int lea_grafo (int grafo[][MAXIMO])
{
int lea(),v,ad,i,j,n,costo;
PR("De numero de vertices...");
SALTO;
n = lea();
for (i=1; i <= n;
i++)
for (j=1; j
<=n; j++)
grafo[i][j]
= 32000;
PR
("Vertice ... ");
v
= 1;
printf
("%d",v);
SALTO;
while
(v <= n) {
PR
("Lea el primer adjunto al vertice ");
printf
("%d ",v);
PR(".
99 para terminar");
SALTO;
ad = lea();
while
(ad != 99) {
PR("Lea
costo del arco");SALTO;
costo
= lea();
grafo
[v][ad] = costo;
PR
("Lea otro adjunto al vertice ");
printf
("%d ",v);
PR(".
99 para terminar");
SALTO;
ad
= lea();
}PR
("Vertice ...");
v++;
printf
("%d ",v);
SALTO;
}return (n);
}int lea() {
char L[10];
gets (L);
return (atoi (L));}
void listar_g (int g[][MAXIMO], int nv) {
int i,j;
for (i=1; i <= nv; i++) {
for (j = 1;
j <= nv; j++)
if
(g[i][j] == 32000)
printf
("%s"," * ");
else
printf ("%2d ",g[i][j]);
SALTO;}}
"El siguiente articulo fue elaborado por un estudiante de Ingeniería de Sistemas de la Universidad Incca de Colombia"
Algoritmo de Dijkstra.
Se le atribuye el nombre al
científico de computación Holandés Edsger Dijkstra, también llamado al
algoritmo de caminos mínimos. Consiste en encontrar el camino más corto entre
dos vértices, cada uno de los vértices debe tener una etiquete y los arcos un
peso. El grafo no debe estar dirigido ya que si lo esta no sería de este tipo.
Primero tomamos un punto de
partida x, este puede ser cualquier vértices y tomamos uno como el punto de
llegada, se toman los vértices adyacentes al origen y se evalúa el de menor
peso, es decir, el que tenga la etiqueta con el número menor, se toma ese
camino y se hace el mismo proceso hasta llegar al vértice que se tomó como
final.
Ejemplo
Calcular la longitud entre a
y g.
Vértice
|
1
|
2
|
3
|
5
|
6
|
a |
[0 , x] |
||||
b
|
[8 –
a]
|
[6 –
d]
|
[10
– e]
|
||
c
|
[5 – a] |
||||
d
|
[3 – c]
|
||||
e
|
|||||
f
|
[7 –
c]
|
[5 –
d]
|
|||
g
|
[1 - e] |
Camino más corto: a, c, d, e, g.
En el anterior cuadro se
puede ver como se aplica el algoritmo de Dijkstra, se inicia en el primer
vértice donde se pone el peso acumulado y el vértice de donde procede al ser el
primero no tienen peso acumulado ni un vértice de procedencia, en la segunda casilla
se toman los vértices adyacente al primero y se compara, el recuadro azul da la
etiqueta definitiva que dice que este es el camino más corto entre los dos
vértices comparados, se realiza hasta el final y obtenemos el camino más corto.
#include "stdio.h"
#include "conio.h"
#include "stdlib.h"
#define MAXIMO 20
#define PR(x) printf
("%s",x)
#define
SALTO printf ("\n")
int
main() {
int
M[MAXIMO][MAXIMO],T[MAXIMO][MAXIMO];
int suma,
marcas[MAXIMO],padres[MAXIMO],minimo [MAXIMO];
int nv,i;
void
DIJKSTRA (int M[][MAXIMO],int N,int minimo[],int padres[],int marcas[]);
void
listar_r (int a[],int nv);
int
lea_grafo (int grafo[][MAXIMO]);
void
listar_g (int g[][MAXIMO], int nv);
nv = lea_grafo (M);
listar_g (M ,nv);
SALTO;
getch();
DIJKSTRA (M,nv,minimo,padres,marcas);
listar_r (minimo,nv);
SALTO;
listar_r (padres,nv);
SALTO;
listar_r (marcas,nv);
SALTO;
getch();
}
void DIJKSTRA (int
M[][MAXIMO],int N,int minimo[],
int padres[],int
marcas[])
{
int min;
int
j,k,escogido;
for
(j=1; j<=N; j++ ) {
minimo[j]
= M[1][j];
marcas [j] = 0;
padres [j] = 1;
}
minimo [1] = 0;
padres [1]= 0;
marcas [1] = 1;
for (k = 2; k <= N; k++) {
min = 32000; /* No puede
ser 32767 para maquinas de 16 bits
para
cada entero. ?Porque?.
Tambien
en la lectura debe ser 32000 */
for (j=1; j <= N; j++)
if
(marcas [j] == 0 && minimo [j] < min) {
min = minimo [j];
escogido
= j;
}
marcas [escogido] = 1;
for (j=1; j <= N;
j++)
if (marcas
[j] == 0 &&
(min
+ M[escogido][j] < minimo[j]) ) {
minimo
[j] = min + M[escogido][j];
padres
[j] = escogido;
}
}
}
int
lea_grafo (int grafo[][MAXIMO])
{
int lea(),v,ad,i,j,n,costo;
PR("De numero de
vertices...");
SALTO;
n = lea();
for
(i=1; i <= n; i++)
for (j=1; j <=n; j++)
grafo[i][j]
= 32000;
PR
("Vertice ... ");
v = 1;
printf ("%d",v);
SALTO;
while (v <= n) {
PR ("Lea el primer
adjunto al vertice ");
printf ("%d
",v);
PR(". 99 para
terminar");
SALTO;
ad = lea();
while (ad != 99) {
PR("Lea
costo del arco");SALTO;
costo =
lea();
grafo [v][ad]
= costo;
PR ("Lea
otro adjunto al vertice ");
printf
("%d ",v);
PR(". 99
para terminar");
SALTO;
ad
= lea();
}
PR
("Vertice ...");
v++;
printf
("%d ",v);
SALTO;
}
return
(n);
}
int lea() {
char
L[10];
gets
(L);
return (atoi (L));
void listar_g (int g[][MAXIMO],
int nv) {
int
i,j;
for
(i=1; i <= nv; i++) {
if
(g[i][j] == 32000)
printf
("%s"," * ");
else
printf ("%2d ",g[i][j]);
SALTO;
}
}
void listar_r (int a[],int nv) {
int
k;
for
(k=1; k<=nv; k++)
printf ("%d
",a[k]);
}






















No hay comentarios.:
Publicar un comentario